The following slides accompanied a presentation delivered at ASHA’s Clinical Practice Research Institute.

Another approach to analyzing data from group comparison studies.
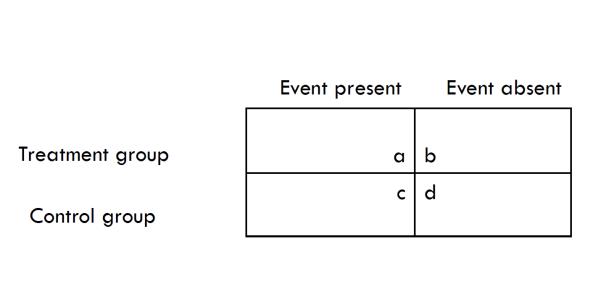
Instead of comparing means, dichotomize the event (outcome) of interest as “present” or “absent” in individual patients within the groups.
Then compare the distribution of events in the experimental group and in the control group.
All studies, no matter how complicated, can be simplified into a 2×2 table. . .a 2×2 table is a simple but powerful tool to communicate information. (Dodson, 2007, p. 307 and p. 312)
Reasons to consider event-based measures (singly or in tandem)

Dichotomizing forces decisions
- What event is important?
- What is threshold for defining the event as “present”?
- How many people must be treated in order for one to experience the positive event?
Event-based measures can enrich and sometimes change the perception of the impact of an experimental treatment or condition.
Two common metrics for comparing event distributions (along with CIs)

Proportions/Probabilities/Rates of occurrence
- # of events/# of people in the group
Odds
- Ratio of events/non-events in the group
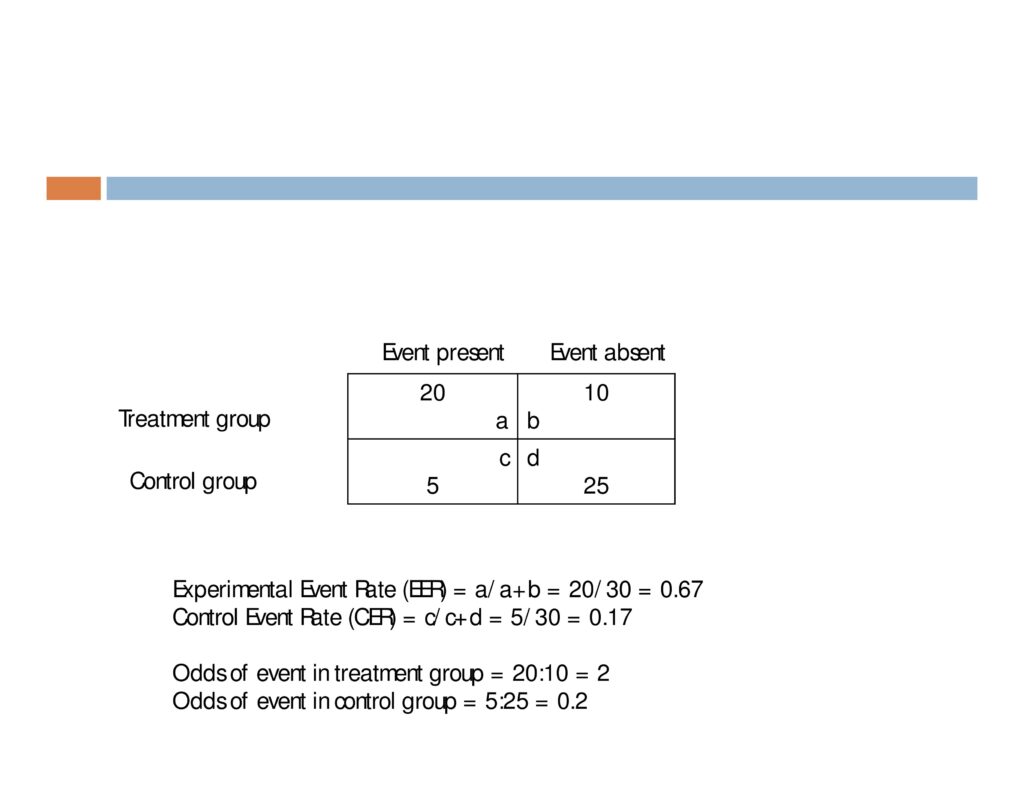
If 30 people receive treatment, and 10 improve
- Proportion who improve with treatment = 10/30 = .33
- Odds of improving with treatment = 10:20 = .50

Proportions/probabilities/rates in experimental and control groups can be compared in
- Raw (absolute) values – simple subtraction of proportions in the two groups
- Relational values: Ratio of the rate of the event in one group to the rate in the other Ratio of the odds of the event in one group to the odds in the other
Odds in the experimental and control groups are typically compared relationally
- Ratio of odds of the event in one group to the odds in the other
2×2 tables – might as well get used to them
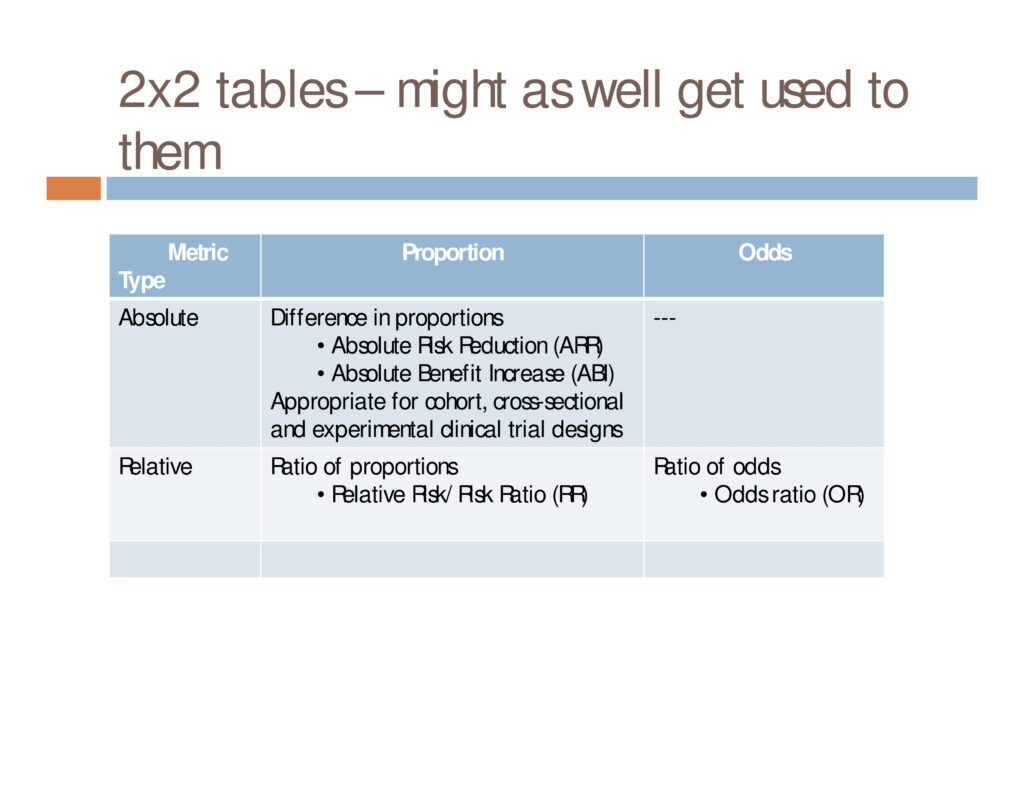
Metric Type: Absolute
Proportion: Difference in proportions
- Absolute Risk Reduction (ARR)
- Absolute Benefit Increase (ABI)
Appropriate for cohort, cross-sectional and experimental clinical trial designs
Metric Type: Relative
Proportion: Relative Ratio of proportions
- Relative Risk/Risk Ratio (RR)
Odds: Ratio of odds
- Odds ratio (OR)
Rates of occurrence (proportions)

Begin with a 2 x 2 contingency table.
Experimental Event Rate = proportion of people in Tx group who had the event = a/a+b
Control Event Rate = proportion of people in Ctrl group who had the event = c/c+d
Absolute difference in proportions

Absolute arithmetic difference in rates of event for each group, i.e., EER – CER
Always between 1.0 group and 1.0; zero if no association between event and -group
When the event of interest is avoiding a poor outcome, the difference in porportions is known as the Absolute Risk Reduction (ARR, or risk difference)
When the event of interest is increasing a good outcome, the difference in proportions is known as the Absolute Benefit Increase (ABI)
A treatment example
See (Gillam et al., 2008).

RCT of 3 types of language intervention and an active control
NSD among group means on primary outcome measures, based on group mean comparisons
Could also examine effects using an event-based metric
- Did the groups differ in the number ofchildren whose scores had moved into the normal range by the end of the study? (desirable outcome)
- Did the groups differ in the number of children whose scores remained in the disordered range at the end of the study? (undesirable outcome
Absolute Risk Reduction (ARR)

Proportion of children who had a poor outcome (language scores remained abnormally low)
- In treatment group (EER): 24.1%
- In control group (CER): 29.6%
ARR = EER – CER = 24.1 – 29.6 = – 5.5%
The probability of a poor outcome was about 5% lower for children in the treatment group than for children in the control group.
Absolute Benefit Increase (ABI)
Proportion of children who had a poor outcome (language scores remained abnormally low)
- In treatment group (EER): 24.1%
- In control group (CER): 29.6%
ARR = EER – CER = 24.1 – 29.6 = – 5.5%
The probability of a poor outcome was about 5% lower for children in the treatment group than for children in the control group.
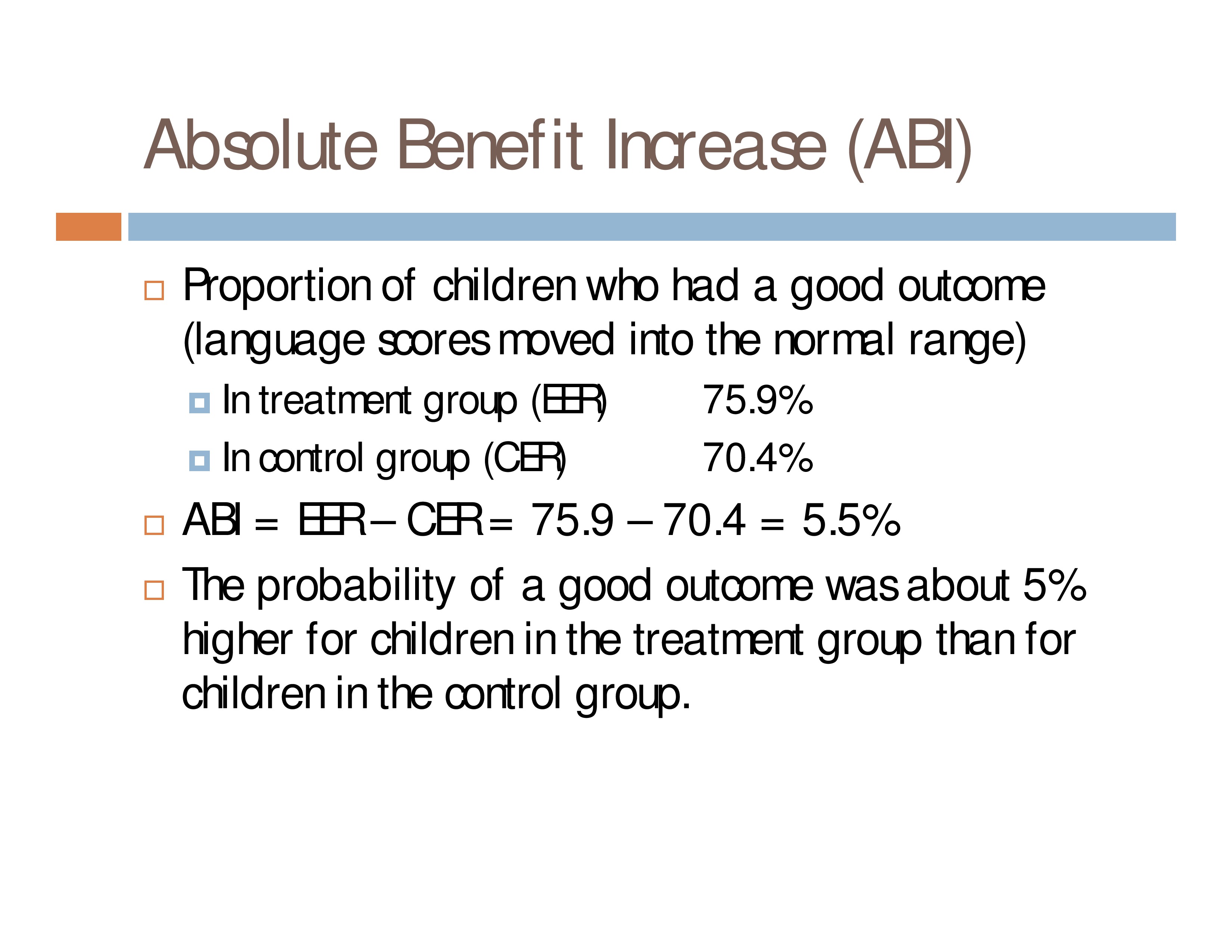
Absolute Benefit Increase (ABI)

Proportion of children who had a good outcome (language scores moved into the normal range)
- In treatment group (EER): 75.9%
- In control group (CER): 70.4%
ABI = EER – CER = 75.9 – 70.4 = 5.5%
The probability of a good outcome was about 5% higher for children in the treatment group than for children in the control group.
Number Needed to Treat (NNT)

The number of patients who would have to be treated for just one of them to experience the beneficial outcome
- 1/ARR (for lowering risk of poor outcome)
- ARR = EER – CER = 24.1 – 29.6 = – 5.5; NNT = 1/5.5 = 18
- 1/ABI (for increasing likelihood of good outcome)
ABI = EER – CER = 75.9 – 70.4 = 5.5; NNT = 1/5.5 = 18
18 children with language impairment would have to be treated with no effect for every 1 child who benefited from the treatment
Interpretation depends on costs, harms, patient values and resources — but with an event-based metric these calculations can be undertaken much more easily.
Number Needed to Harm (NNH)

Identical logic, but event of interest is a harm rather than a benefit
1/Absolute risk increase
We haven’t usually considered harms for behavioral treatments (the assumption of benefit is difficult to escape!)
But harms may be psychological, social, emotional, financial (for patient, family and society)
There are no free lunches: resources ($$) allocated to ineffective and/or harmful treatments could have been used for other problems or treatments
Relational Rate Metrics: Relative Risk

The ratio of the event rate in the experimental group (EER) to the event rate in the control group (CER): i.e., [a/(a+b)] / [c/(c+d)]
Value can be any non-negative number; if value is 1.0 there no association between event and group
If value is 2.0, the event was twice as likely in experimental group as in control group
An example from a prediction study

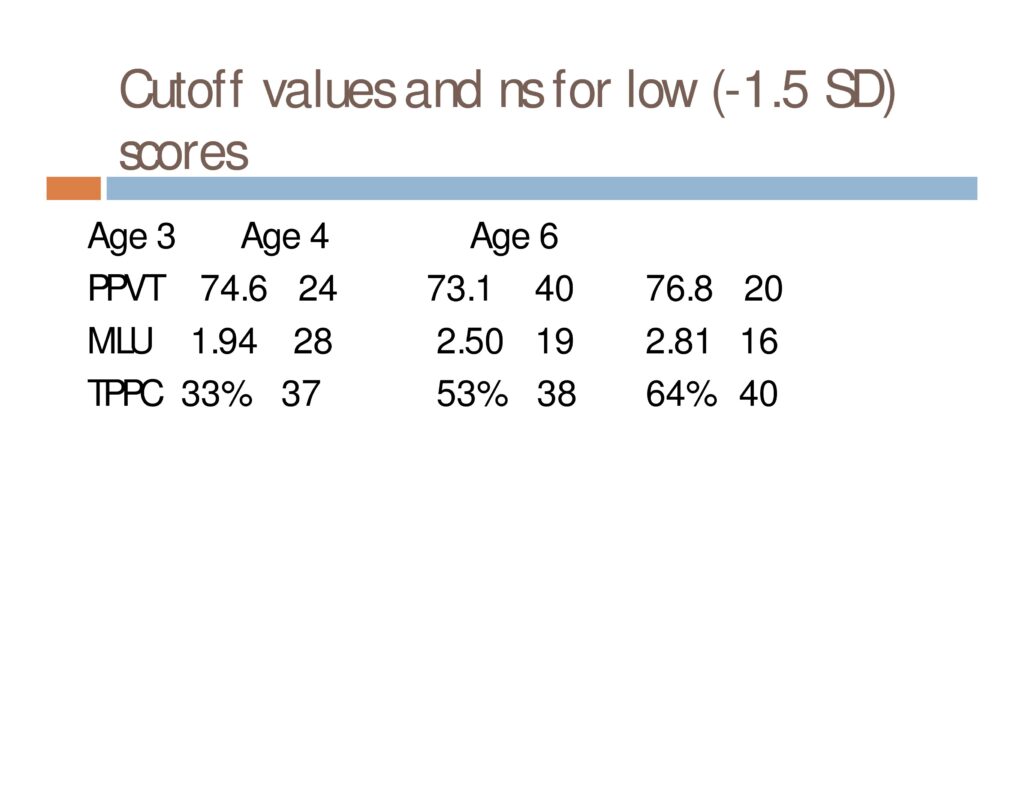
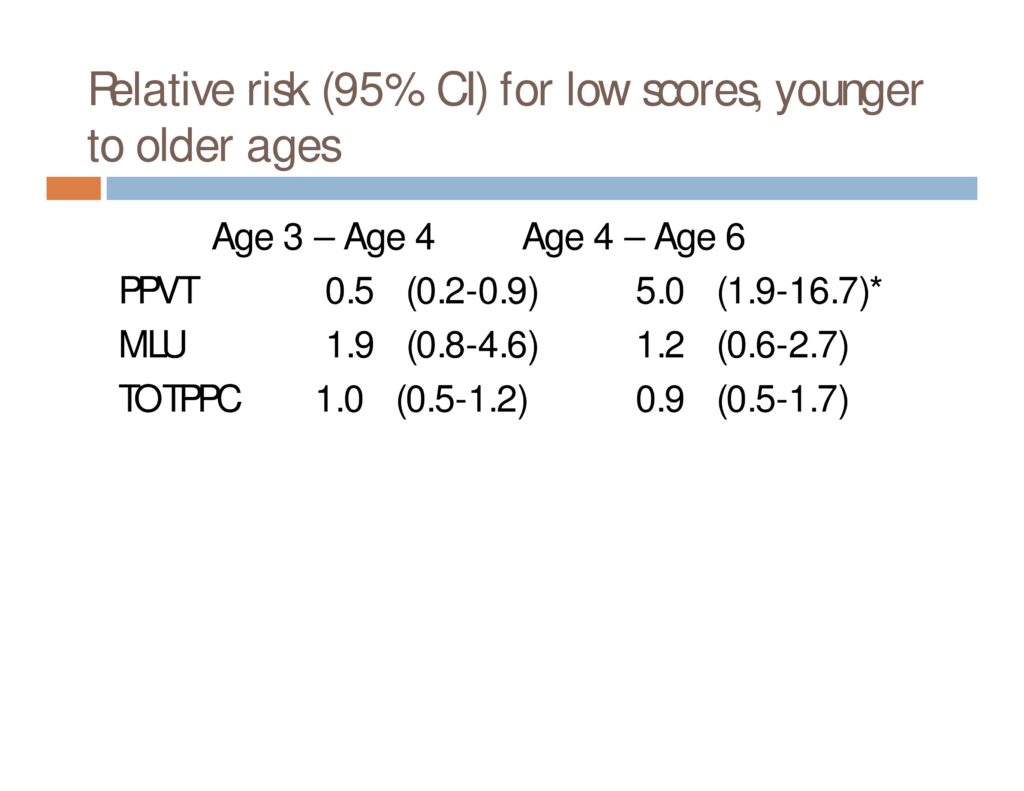
Do children who obtain low scores on a language measure at one age have an increased risk of low scores on the same measure at a later age, as compared to children who had scores WNL?
An example from a cohort study

N = 414 children with complete data sets (3 measures at each of 3 ages) from a cohort of 782 who were followed longitudinally for another study
50% male; 11% had mothers who were not high school graduates
No significant neonatal medical history; monolingual English-speaking families
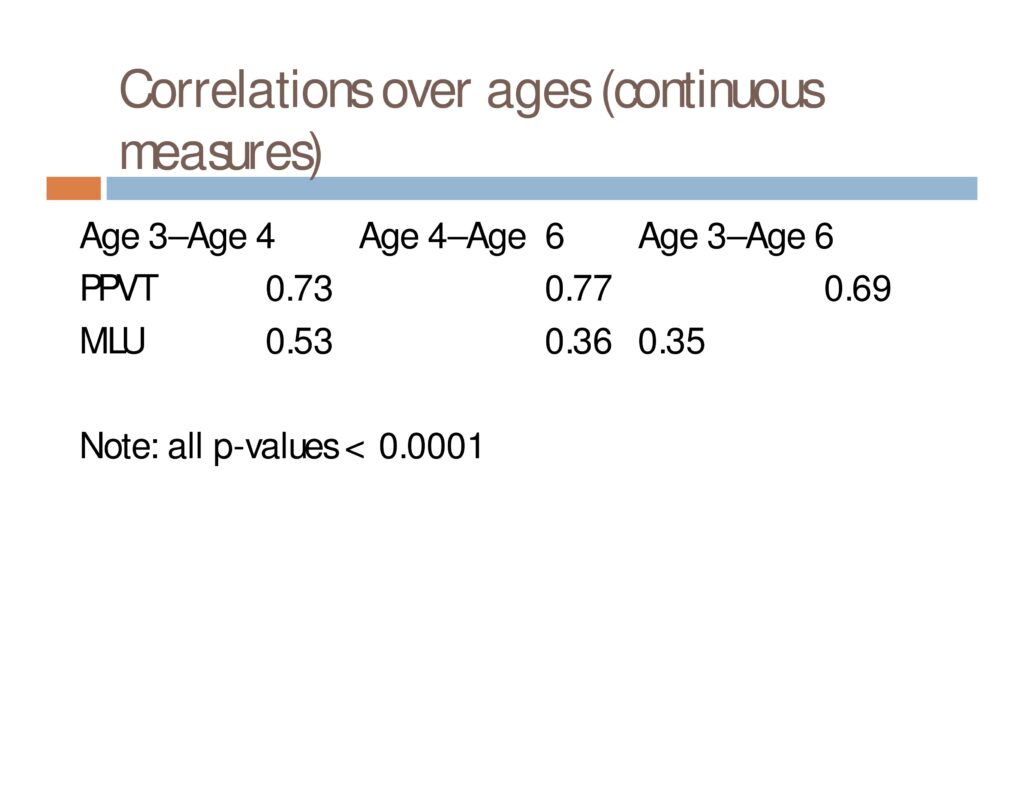
Measures: Peabody Picture Vocabulary Test, Mean Length of Utterance, Nonword
Repetition Task: Total Percentage Phonemes Correct
Final Thoughts

Correlations tell us one story.
Event distributions deepen our understanding of that story.

References
Dodson, T.B. (2007). A guide for preparing a patientoriented manuscript. Oral Surgery, Oral Medicine, Oral Pathology, Oral Radiology, and Endodontology, 104, 307–315. [Article]
Gillam, R.B., Frome Loeb, D., Hoffman, L.M., Bohman, T., Champlin, C.A., Thibodeau, L., Widen, J., Brandel, J. & Friel-Patti, S. (2008). The efficacy of Fast ForWord language intervention in school-age children with language impairment: A randomized controlled trial. J Speech Lang Hear Res, 51, 97–119. [Article] [PubMed]
Sistrom, C.L. & Garvan, C.W. (2004). Proportions, odds, and risk. Radiology, 230, 12–19. [Article] [PubMed]